Spis treści
W tej publikacji rozważymy jedno z głównych twierdzeń teorii liczb całkowitych – Małe twierdzenie Fermatanazwany na cześć francuskiego matematyka Pierre'a de Fermata. Przeanalizujemy również przykład rozwiązania problemu, aby utrwalić przedstawiony materiał.
Stwierdzenie twierdzenia
1. Początkowa
If p jest liczbą pierwszą a jest liczbą całkowitą niepodzielną przez pnastępnie ap-1 - 1 podzielone przez p.
Formalnie jest napisany tak: ap-1 1 (przeciwko p).
Uwaga: Liczba pierwsza to liczba naturalna, która jest podzielna tylko przez XNUMX i samą siebie bez reszty.
Na przykład:
- a = 2
- p = 5
- ap-1 - 1 = 25 - 1 - 1 = 24 – 1 = 16 – 1 = 15
- numer 15 podzielone przez 5 bez reszty.
2. Alternatywa
If p jest liczbą pierwszą, a dowolna liczba całkowita, to ap porównywalny do a Modulo p.
ap a (przeciwko p)
Historia znajdowania dowodów
Pierre de Fermat sformułował twierdzenie w 1640 r., ale sam go nie udowodnił. Później zrobił to Gottfried Wilhelm Leibniz, niemiecki filozof, logik, matematyk itp. Uważa się, że dowód ten miał już w 1683 r., chociaż nigdy go nie opublikowano. Warto zauważyć, że Leibniz sam odkrył twierdzenie, nie wiedząc, że zostało już wcześniej sformułowane.
Pierwszy dowód twierdzenia został opublikowany w 1736 roku i należy do Szwajcara, Niemca oraz matematyka i mechanika Leonharda Eulera. Małe Twierdzenie Fermata jest szczególnym przypadkiem twierdzenia Eulera.
Przykład problemu
Znajdź resztę liczby 212 on 12.
Rozwiązanie
Wyobraźmy sobie numer 212 as 2⋅211.
11 jest liczbą pierwszą, dlatego z małego twierdzenia Fermata otrzymujemy:
211 2 (przeciwko 11).
Stąd, 2⋅211 4 (przeciwko 11).
Więc liczba 212 podzielone przez 12 z resztą równą 4.










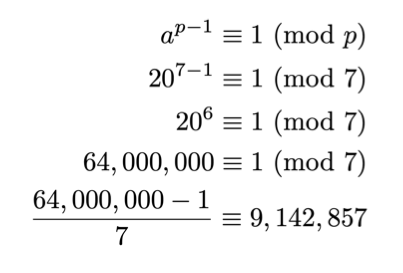
a ile p qarsiliqli sade olmalidir
+ yazilan melumatlar tam basa dusulmur. ingilis dilinden duzgun tercume ounmayib