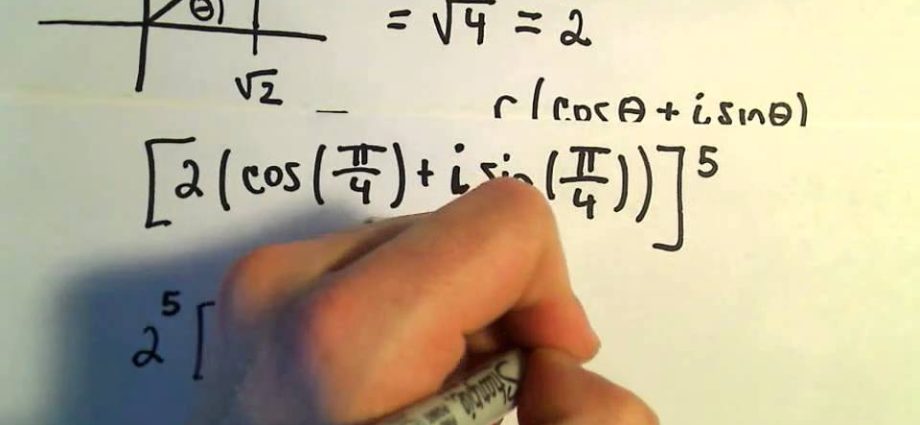Podnoszenie liczby zespolonej do naturalnej potęgi

W tej publikacji zastanowimy się, jak liczbę zespoloną można podnieść do potęgi (w tym za pomocą wzoru De Moivre). Materiałowi teoretycznemu towarzyszą przykłady dla lepszego zrozumienia.

Podnoszenie liczby zespolonej do potęgi

Po pierwsze, pamiętaj, że liczba zespolona ma postać ogólną: z = a + bi (forma algebraiczna).

Teraz możemy przejść bezpośrednio do rozwiązania problemu.

Numer kwadratowy

Możemy przedstawić stopień jako iloczyn tych samych czynników, a następnie znaleźć ich iloczyn (pamiętając o tym) i² = -1).

z² = (a + bi)² = (a + bi) (a + bi)

1 przykład:

z=3+5i

z² = (3 + 5i)² = (3 + 5i)(3 + 5i) = 9 + 15i + 15i + 25i² = -16 + 30i

Możesz również użyć, a mianowicie kwadrat sumy:

z² = (a + bi)² = a² + 2 ⋅ za ⋅ bi + (bi)² = a² + 2abi – ur²

Uwaga: W ten sam sposób, jeśli to konieczne, można uzyskać wzory na kwadrat różnicy, sześcian sumy / różnicy itp.

N-ty stopień

Podnieś liczbę zespoloną z w naturze n znacznie łatwiej, jeśli jest reprezentowany w formie trygonometrycznej.

Przypomnijmy, że ogólnie zapis liczby wygląda tak: z = |z| ⋅ (cos φ + i ⋅ grzech φ).

Do potęgowania możesz użyć Formuła de Moivre'a (tak nazwany na cześć angielskiego matematyka Abrahama de Moivre):

zⁿ = | z |ⁿ ⋅ (cos(nφ) + i ⋅ grzech(nφ))

Wzór otrzymujemy pisząc w formie trygonometrycznej (moduły są mnożone, a argumenty dodawane).

2 przykład

Podnieś liczbę zespoloną z = 2 ⋅ (cos 35° + i ⋅ grzech 35°) do ósmego stopnia.

Rozwiązanie

z⁸ = 2⁸ ⋅ (cos(8 ⋅ 35°) + i ⋅ grzech(8 ⋅ 35°)) = 256 ⋅ (cos 280° + i grzech 280°).